Multiples and Factors

http://mrsrclassroom.weebly.com/factors-and-multiples.html

Multiples and Factors Song


Finding Factors using a factor rainbow
https://www.chilimath.com/lessons/introductory-algebra/finding-all-the-factors-of-a-whole-number-using-the-rainbow-method/

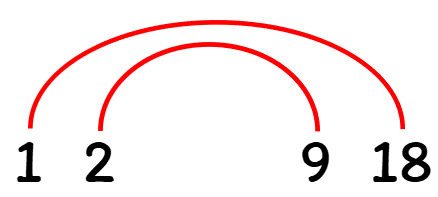
Step 1: The first number that you with is 1. 1 will ALWAYS be a factor of any number and its pair will ALWAYS be the number itself. You write the two numbers with a space between them. 

the first factor on the rainbow diagram is 1 and 18

Step 2: Then you move onto the next number which is 2. If 2 can go into the number evenly then it is a factor. You then find its pairing and write the pairings, again leaving a space in between them. 

the second factor pair of the rainbow diagram is 2 and 9

Step 3: You move onto 3.  If 3 can go into the number evenly then it is a factor. You then find its pairing and write the pairings, again leaving a space in between them. 

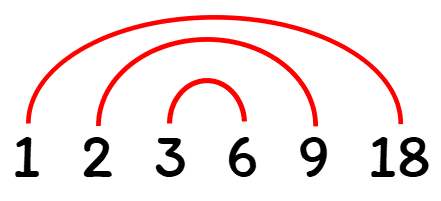
the third factor pair in the rainbow diagram is 3 and 6

Step 4: You then keep moving on to the next number. If the next number does not go into your chosen number evenly then it is not a factor so you move on to the next number. 


Step 5: You stop when the next number on your list already has a pair in your rainbow. You have now found all the factors for your number. 

the third factor pair in the rainbow diagram is 3 and 6

All the factors of 18 are: 1, 2, 3, 6, 9 and 18

Lowest Common Multiple

Lowest Common Multiple (LCM): when 2 sets of numbers are being compared, this is the lowest multiple both numbers have in common.

For example: The Lowest Common Multiple of 2 and 3 is 6:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 18
- Multiples of 3: 3, 6, 9, 12, 15, 18

Greatest Common Factor

Greatest Common Factor (GCF): when two sets of numbers are being compared, this is the greatest factor both numbers have in common.

For example: The Greatest common factor of 12 and 18 is 6:
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 18: 1, 2, 3, 6, 9, 18
               

Comments

Post a Comment

Popular posts from this blog

Welcome to the 6-4 blog!

Week of May 11th to 14th This week is a shorter week as there is no school on Friday or Monday! So you all have a nice long weekend next week! Here is our plan for the week, all your assignments this week will be due next Monday 18th. Google meet: Tuesday at 1pm LA: I have uploaded the next four chapter of Among the Imposters (chapters 14-17). There is a comprehension question to answer so click on the link to access it. LA: Writing assignment "Meet my Furry Friend". Please read all the instructions to know what to do and modifications that can be made. Science: What is air collage? Please create a visual collage of everything you know about air. You can include things that you already know or do some research to find out more information. THINK about what our BIG QUESTION was this year! Math: For this week I have just added some practice that you can do if you feel that you may need it before we move onto the next part of fractions. Fill The We
Read more